7.7-DP-day1
本文最后更新于 2024年10月21日 早上
动态规划理论基础
什么是动态规划
动态规划,英文:Dynamic Programming,简称DP,如果某一问题有很多重叠子问题,使用动态规划是最有效的。
所以动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心,贪心没有状态推导,而是从局部直接选最优的
在关于贪心算法,你该了解这些! (opens new window)中我举了一个背包问题的例子。
例如:有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i],得到的价值是value[i]。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
动态规划中dp[j]是由dp[j-weight[i]]推导出来的,然后取max(dp[j], dp[j - weight[i]] + value[i])。
但如果是贪心呢,每次拿物品选一个最大的或者最小的就完事了,和上一个状态没有关系。
所以贪心解决不了动态规划的问题。
其实大家也不用死扣动规和贪心的理论区别,后面做做题目自然就知道了。
而且很多讲解动态规划的文章都会讲最优子结构啊和重叠子问题啊这些,这些东西都是教科书的上定义,晦涩难懂而且不实用。
大家知道动规是由前一个状态推导出来的,而贪心是局部直接选最优的,对于刷题来说就够用了。
上述提到的背包问题,后序会详细讲解。
动态规划的解题步骤
做动规题目的时候,很多同学会陷入一个误区,就是以为把状态转移公式背下来,照葫芦画瓢改改,就开始写代码,甚至把题目AC之后,都不太清楚dp[i]表示的是什么。
这就是一种朦胧的状态,然后就把题给过了,遇到稍稍难一点的,可能直接就不会了,然后看题解,然后继续照葫芦画瓢陷入这种恶性循环中。
状态转移公式(递推公式)是很重要,但动规不仅仅只有递推公式。
对于动态规划问题,我将拆解为如下五步曲,这五步都搞清楚了,才能说把动态规划真的掌握了!
[!TIP]
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
一些同学可能想为什么要先确定递推公式,然后在考虑初始化呢?
因为一些情况是递推公式决定了dp数组要如何初始化!
后面的讲解中我都是围绕着这五点来进行讲解。
可能刷过动态规划题目的同学可能都知道递推公式的重要性,感觉确定了递推公式这道题目就解出来了。
其实 确定递推公式 仅仅是解题里的一步而已!
一些同学知道递推公式,但搞不清楚dp数组应该如何初始化,或者正确的遍历顺序,以至于记下来公式,但写的程序怎么改都通过不了。
后序的讲解的大家就会慢慢感受到这五步的重要性了。
动态规划应该如何debug
相信动规的题目,很大部分同学都是这样做的。
看一下题解,感觉看懂了,然后照葫芦画瓢,如果能正好画对了,万事大吉,一旦要是没通过,就怎么改都通过不了,对 dp数组的初始化,递推公式,遍历顺序,处于一种黑盒的理解状态。
写动规题目,代码出问题很正常!
找问题的最好方式就是把dp数组打印出来,看看究竟是不是按照自己思路推导的!
一些同学对于dp的学习是黑盒的状态,就是不清楚dp数组的含义,不懂为什么这么初始化,递推公式背下来了,遍历顺序靠习惯就是这么写的,然后一鼓作气写出代码,如果代码能通过万事大吉,通过不了的话就凭感觉改一改。
这是一个很不好的习惯!
做动规的题目,写代码之前一定要把状态转移在dp数组的上具体情况模拟一遍,心中有数,确定最后推出的是想要的结果。
然后再写代码,如果代码没通过就打印dp数组,看看是不是和自己预先推导的哪里不一样。
如果打印出来和自己预先模拟推导是一样的,那么就是自己的递归公式、初始化或者遍历顺序有问题了。
如果和自己预先模拟推导的不一样,那么就是代码实现细节有问题。
这样才是一个完整的思考过程,而不是一旦代码出问题,就毫无头绪的东改改西改改,最后过不了,或者说是稀里糊涂的过了。
这也是我为什么在动规五步曲里强调推导dp数组的重要性。
举个例子哈:在「代码随想录」刷题小分队微信群里,一些录友可能代码通过不了,会把代码抛到讨论群里问:我这里代码都已经和题解一模一样了,为什么通过不了呢?
发出这样的问题之前,其实可以自己先思考这三个问题:
- 这道题目我举例推导状态转移公式了么?
- 我打印dp数组的日志了么?
- 打印出来了dp数组和我想的一样么?
如果这灵魂三问自己都做到了,基本上这道题目也就解决了,或者更清晰的知道自己究竟是哪一点不明白,是状态转移不明白,还是实现代码不知道该怎么写,还是不理解遍历dp数组的顺序。
然后在问问题,目的性就很强了,群里的小伙伴也可以快速知道提问者的疑惑了。
注意这里不是说不让大家问问题哈, 而是说问问题之前要有自己的思考,问题要问到点子上!
大家工作之后就会发现,特别是大厂,问问题是一个专业活,是的,问问题也要体现出专业!
如果问同事很不专业的问题,同事们会懒的回答,领导也会认为你缺乏思考能力,这对职场发展是很不利的。
所以大家在刷题的时候,就锻炼自己养成专业提问的好习惯。
总结
这一篇是动态规划的整体概述,讲解了什么是动态规划,动态规划的解题步骤,以及如何debug。
动态规划是一个很大的领域,今天这一篇讲解的内容是整个动态规划系列中都会使用到的一些理论基础。
在后序讲解中针对某一具体问题,还会讲解其对应的理论基础,例如背包问题中的01背包,leetcode上的题目都是01背包的应用,而没有纯01背包的问题,那么就需要在把对应的理论知识讲解一下。
大家会发现,我讲解的理论基础并不是教科书上各种动态规划的定义,错综复杂的公式。
这里理论基础篇已经是非常偏实用的了,每个知识点都是在解题实战中非常有用的内容,大家要重视起来哈。
509. 斐波那契数
题意描述:
[!NOTE]
斐波那契数 (通常用
F(n)表示)形成的序列称为 斐波那契数列 。该数列由0和1开始,后面的每一项数字都是前面两项数字的和。也就是:
2F(0) = 0,F(1) = 1
F(n) = F(n - 1) + F(n - 2),其中 n > 1给定
n,请计算F(n)。示例 1:
2
3输入:n = 2
输出:1
解释:F(2) = F(1) + F(0) = 1 + 0 = 1示例 2:
2
3输入:n = 3
输出:2
解释:F(3) = F(2) + F(1) = 1 + 1 = 2示例 3:
2
3输入:n = 4
输出:3
解释:F(4) = F(3) + F(2) = 2 + 1 = 3提示:
0 <= n <= 30
思路:
[!TIP]
斐波那契数列大家应该非常熟悉不过了,非常适合作为动规第一道题目来练练手。
因为这道题目比较简单,可能一些同学并不需要做什么分析,直接顺手一写就过了。
但「代码随想录」的风格是:简单题目是用来加深对解题方法论的理解的。
通过这道题目让大家可以初步认识到,按照动规五部曲是如何解题的。
对于动规,如果没有方法论的话,可能简单题目可以顺手一写就过,难一点就不知道如何下手了。
所以我总结的动规五部曲,是要用来贯穿整个动态规划系列的,就像之前讲过二叉树系列的递归三部曲 (opens new window),回溯法系列的回溯三部曲 (opens new window)一样。后面慢慢大家就会体会到,动规五部曲方法的重要性。
动态规划
动规五部曲:
这里我们要用一个一维
dp数组来保存递归的结果
- 确定
dp数组以及下标的含义
dp[i]的定义为:第i个数的斐波那契数值是dp[i]
- 确定递推公式
为什么这是一道非常简单的入门题目呢?
因为题目已经把递推公式直接给我们了:状态转移方程
dp[i] = dp[i - 1] + dp[i - 2];
- dp数组如何初始化
题目中把如何初始化也直接给我们了,如下:
2dp[0] = 0;
dp[1] = 1;
- 确定遍历顺序
从递归公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,dp[i]是依赖 dp[i - 1] 和 dp[i - 2],那么遍历的顺序一定是
从前到后遍历的
- 举例推导dp数组
按照这个递推公式dp[i] = dp[i - 1] + dp[i - 2],我们来推导一下,当N为10的时候,dp数组应该是如下的数列:
0 1 1 2 3 5 8 13 21 34 55
如果代码写出来,发现结果不对,就把dp数组打印出来看看和我们推导的数列是不是一致的。
以上我们用动规的方法分析完了,C++代码如下:
2
3
4
5
6
7
8
9
10
11
12
13class Solution {
public:
int fib(int N) {
if (N <= 1) return N;
vector<int> dp(N + 1);
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= N; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[N];
}
};
- 时间复杂度:O(n)
- 空间复杂度:O(n)
当然可以发现,我们只需要维护两个数值就可以了,不需要记录整个序列。
代码如下:
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
int fib(int N) {
if (N <= 1) return N;
int dp[2];
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= N; i++) {
int sum = dp[0] + dp[1];
dp[0] = dp[1];
dp[1] = sum;
}
return dp[1];
}
};
- 时间复杂度:O(n)
- 空间复杂度:O(1)
递归解法(代价大不推荐)
本题还可以使用递归解法来做
代码如下:
2
3
4
5
6
7class Solution {
public:
int fib(int N) {
if (N < 2) return N;
return fib(N - 1) + fib(N - 2);
}
};
- 时间复杂度:O(2^n)
- 空间复杂度:O(n),算上了编程语言中实现递归的系统栈所占空间
这个递归的时间复杂度大家画一下树形图就知道了,如果不清晰的同学,可以看这篇:通过一道面试题目,讲一讲递归算法的时间复杂度!(opens new window)
总结
斐波那契数列这道题目是非常基础的题目,我在后面的动态规划的讲解中将会多次提到斐波那契数列!
这里我严格按照关于动态规划,你该了解这些! (opens new window)中的动规五部曲来分析了这道题目,一些分析步骤可能同学感觉没有必要搞的这么复杂,代码其实上来就可以撸出来。
但我还是强调一下,简单题是用来掌握方法论的,动规五部曲将在接下来的动态规划讲解中发挥重要作用,敬请期待!
70. 爬楼梯
题意描述:
[!NOTE]
假设你正在爬楼梯。需要
n阶你才能到达楼顶。每次你可以爬
1或2个台阶。你有多少种不同的方法可以爬到楼顶呢?示例 1:
2
3
4
5输入:n = 2
输出:2
解释:有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶示例 2:
2
3
4
5
6输入:n = 3
输出:3
解释:有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶提示:
1 <= n <= 45
思路:
[!TIP]
本题大家如果没有接触过的话,会感觉比较难,多举几个例子,就可以发现其规律。
爬到第一层楼梯有一种方法,爬到二层楼梯有两种方法。
那么第一层楼梯再跨两步就到第三层 ,第二层楼梯再跨一步就到第三层。
所以到第三层楼梯的状态可以由第二层楼梯 和 到第一层楼梯状态推导出来,那么就可以想到动态规划了。
我们来分析一下,动规五部曲:
定义一个一维数组来记录不同楼层的状态
- 确定
dp数组以及下标的含义
dp[i]: 爬到第i层楼梯,有dp[i]种方法
- 确定递推公式
如何可以推出dp[i]呢?
从dp[i]的定义可以看出,dp[i] 可以有两个方向推出来。
首先是dp[i - 1],上i-1层楼梯,有dp[i - 1]种方法,那么再一步跳一个台阶不就是dp[i]了么。
还有就是dp[i - 2],上i-2层楼梯,有dp[i - 2]种方法,那么再一步跳两个台阶不就是dp[i]了么。
那么dp[i]就是 dp[i - 1]与dp[i - 2]之和!
所以
dp[i] = dp[i - 1] + dp[i - 2]。在推导dp[i]的时候,一定要时刻想着dp[i]的定义,否则容易跑偏。
这体现出确定dp数组以及下标的含义的重要性!
- dp数组如何初始化
再回顾一下dp[i]的定义:爬到第i层楼梯,有dp[i]种方法。
那么i为0,dp[i]应该是多少呢,这个可以有很多解释,但基本都是直接奔着答案去解释的。
例如强行安慰自己爬到第0层,也有一种方法,什么都不做也就是一种方法即:dp[0] = 1,相当于直接站在楼顶。
但总有点牵强的成分。
那还这么理解呢:我就认为跑到第0层,方法就是0啊,一步只能走一个台阶或者两个台阶,然而楼层是0,直接站楼顶上了,就是不用方法,dp[0]就应该是0.
其实这么争论下去没有意义,大部分解释说dp[0]应该为1的理由其实是因为dp[0]=1的话在递推的过程中i从2开始遍历本题就能过,然后就往结果上靠去解释dp[0] = 1。
从dp数组定义的角度上来说,dp[0] = 0 也能说得通。
需要注意的是:题目中说了n是一个正整数,题目根本就没说n有为0的情况。
所以本题其实就不应该讨论dp[0]的初始化!
我相信dp[1] = 1,dp[2] = 2,这个初始化大家应该都没有争议的。
所以我的原则是:不考虑dp[0]如何初始化,只初始化dp[1] = 1,dp[2] = 2,然后从i = 3开始递推,这样才符合dp[i]的定义。
- 确定遍历顺序
从递推公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,遍历顺序一定是从前向后遍历的
- 举例推导dp数组
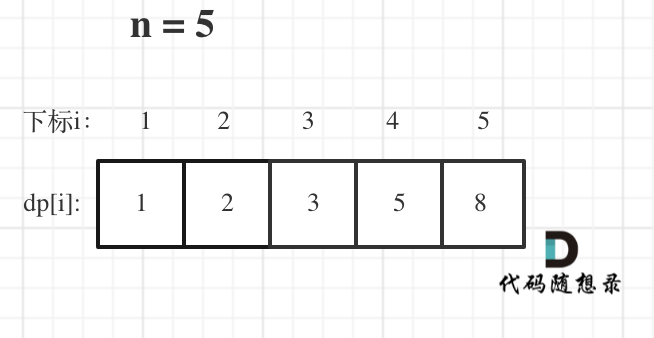
举例当n为5的时候,dp table(dp数组)应该是这样的
如果代码出问题了,就把dp table 打印出来,看看究竟是不是和自己推导的一样。
此时大家应该发现了,这不就是斐波那契数列么!
唯一的区别是,没有讨论dp[0]应该是什么,因为dp[0]在本题没有意义!
以上五部分析完之后,C++代码如下:
2
3
4
5
6
7
8
9
10
11
12
13
14// 版本一
class Solution {
public:
int climbStairs(int n) {
if (n <= 1) return n; // 因为下面直接对dp[2]操作了,防止空指针
vector<int> dp(n + 1);
dp[1] = 1;
dp[2] = 2;
for (int i = 3; i <= n; i++) { // 注意i是从3开始的
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
};
- 时间复杂度:$O(n)$
- 空间复杂度:$O(n)$
当然依然也可以,优化一下空间复杂度,代码如下:
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16// 版本二
class Solution {
public:
int climbStairs(int n) {
if (n <= 1) return n;
int dp[3];
dp[1] = 1;
dp[2] = 2;
for (int i = 3; i <= n; i++) {
int sum = dp[1] + dp[2];
dp[1] = dp[2];
dp[2] = sum;
}
return dp[2];
}
};
- 时间复杂度:$O(n)$
- 空间复杂度:$O(1)$
后面将讲解的很多动规的题目其实都是当前状态依赖前两个,或者前三个状态,都可以做空间上的优化,但我个人认为面试中能写出版本一就够了哈,清晰明了,如果面试官要求进一步优化空间的话,我们再去优化。
因为版本一才能体现出动规的思想精髓,递推的状态变化。
拓展
这道题目还可以继续深化,就是一步一个台阶,两个台阶,三个台阶,直到 m个台阶,有多少种方法爬到n阶楼顶。
这又有难度了,这其实是一个完全背包问题,但力扣上没有这种题目,大家可以去卡码网去做一下 57. 爬楼梯(opens new window)
所以后续我在讲解背包问题的时候,今天这道题还会从背包问题的角度上来再讲一遍。 如果想提前看一下,可以看这篇:70.爬楼梯完全背包版本(opens new window)
这里我先给出本题的代码:
2
3
4
5
6
7
8
9
10
11
12
13class Solution {
public:
int climbStairs(int n) {
vector<int> dp(n + 1, 0);
dp[0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) { // 把m换成2,就可以AC爬楼梯这道题
if (i - j >= 0) dp[i] += dp[i - j];
}
}
return dp[n];
}
};代码中m表示最多可以爬m个台阶。
以上代码不能运行哈,我主要是为了体现只要把m换成2,粘过去,就可以AC爬楼梯这道题,不信你就粘一下试试。
此时我就发现一个绝佳的大厂面试题,第一道题就是单纯的爬楼梯,然后看候选人的代码实现,如果把
dp[0]的定义成1了,就可以发难了,为什么dp[0]一定要初始化为1,此时可能候选人就要强行给dp[0]应该是1找各种理由。那这就是一个考察点了,对dp[i]的定义理解的不深入。(答:dp[0]没有意义。)然后可以继续发难,如果一步一个台阶,两个台阶,三个台阶,直到 m个台阶,有多少种方法爬到n阶楼顶。这道题目leetcode上并没有原题,绝对是考察候选人算法能力的绝佳好题。
这一连套问下来,候选人算法能力如何,面试官心里就有数了。
其实大厂面试最喜欢的问题就是这种简单题,然后慢慢变化,在小细节上考察候选人。
总结
这道题目和动态规划:斐波那契数 (opens new window)题目基本是一样的,但是会发现本题相比动态规划:斐波那契数 (opens new window)难多了,为什么呢?
关键是 动态规划:斐波那契数 (opens new window)题目描述就已经把动规五部曲里的递归公式和如何初始化都给出来了,剩下几部曲也自然而然的推出来了。
而本题,就需要逐个分析了,大家现在应该初步感受出关于动态规划,你该了解这些! (opens new window)里给出的动规五部曲了。
简单题是用来掌握方法论的,例如昨天斐波那契的题目够简单了吧,但昨天和今天可以使用一套方法分析出来的,这就是方法论!
所以不要轻视简单题,那种凭感觉就刷过去了,其实和没掌握区别不大,只有掌握方法论并说清一二三,才能触类旁通,举一反三哈!
746. 使用最小花费爬楼梯
题意描述:
[!NOTE]
给你一个整数数组
cost,其中cost[i]是从楼梯第i个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。你可以选择从下标为
0或下标为1的台阶开始爬楼梯。请你计算并返回达到楼梯顶部的最低花费。
示例 1:
2
3
4
5输入:cost = [10,15,20]
输出:15
解释:你将从下标为 1 的台阶开始。
- 支付 15 ,向上爬两个台阶,到达楼梯顶部。
总花费为 15 。示例 2:
2
3
4
5
6
7
8
9
10输入:cost = [1,100,1,1,1,100,1,1,100,1]
输出:6
解释:你将从下标为 0 的台阶开始。
- 支付 1 ,向上爬两个台阶,到达下标为 2 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 4 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 6 的台阶。
- 支付 1 ,向上爬一个台阶,到达下标为 7 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 9 的台阶。
- 支付 1 ,向上爬一个台阶,到达楼梯顶部。
总花费为 6 。提示:
2 <= cost.length <= 10000 <= cost[i] <= 999
思路:
[!TIP]
(在力扣修改了题目描述下,我又重新修改了题解)
修改之后的题意就比较明确了,题目中说 “你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯” 也就是相当于 跳到 下标 0 或者 下标 1 是不花费体力的, 从 下标 0 下标1 开始跳就要花费体力了。
- 确定dp数组以及下标的含义
使用动态规划,就要有一个数组来记录状态,本题只需要一个一维数组dp[i]就可以了。
dp[i]的定义:到达第i台阶所花费的最少体力为dp[i]。
对于dp数组的定义,大家一定要清晰!
- 确定递推公式
可以有两个途径得到dp[i],一个是
dp[i-1]一个是dp[i-2]。dp[i - 1] 跳到 dp[i] 需要花费
dp[i - 1] + cost[i - 1]。dp[i - 2] 跳到 dp[i] 需要花费
dp[i - 2] + cost[i - 2]。那么究竟是选从
dp[i - 1]跳还是从dp[i - 2]跳呢?一定是选最小的,所以
dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
- dp数组如何初始化
看一下递归公式,
dp[i]由dp[i - 1],dp[i - 2]推出,既然初始化所有的dp[i]是不可能的,那么只初始化dp[0]和dp[1]就够了,其他的最终都是dp[0]、dp[1]推出。那么 dp[0] 应该是多少呢? 根据dp数组的定义,到达第0台阶所花费的最小体力为dp[0],那么有同学可能想,那dp[0] 应该是 cost[0],例如 cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] 的话,dp[0] 就是 cost[0] 应该是1。
这里就要说明本题力扣为什么改题意,而且修改题意之后 就清晰很多的原因了。
新题目描述中明确说了 “你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。” 也就是说 到达 第 0 个台阶是不花费的,但从 第0 个台阶 往上跳的话,需要花费 cost[0]。
所以初始化
dp[0] = 0,dp[1] = 0;
- 确定遍历顺序
最后一步,递归公式有了,初始化有了,如何遍历呢?
本题的遍历顺序其实比较简单,简单到很多同学都忽略了思考这一步直接就把代码写出来了。
因为是模拟台阶,而且dp[i]由
dp[i-1]、dp[i-2]推出,所以是从前到后遍历cost数组就可以了。但是稍稍有点难度的动态规划,其遍历顺序并不容易确定下来。 例如:01背包,都知道两个for循环,一个for遍历物品嵌套一个for遍历背包容量,那么为什么不是一个for遍历背包容量嵌套一个for遍历物品呢? 以及在使用一维dp数组的时候遍历背包容量为什么要倒序呢?
这些都与遍历顺序息息相关。当然背包问题后续「代码随想录」都会重点讲解的!
- 举例推导dp数组
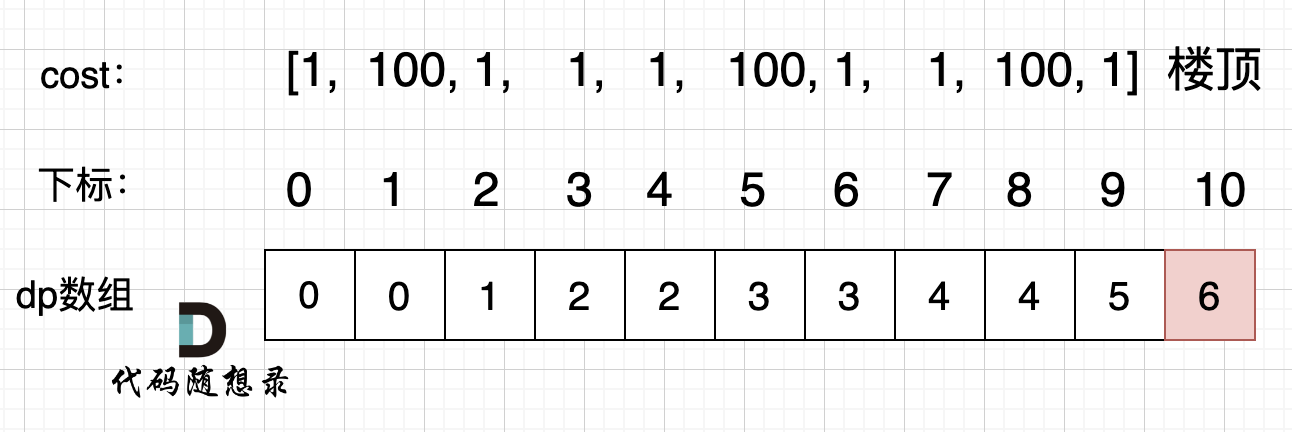
拿示例2:
cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1],来模拟一下dp数组的状态变化,如下:
如果大家代码写出来有问题,就把dp数组打印出来,看看和如上推导的是不是一样的。
以上分析完毕,整体C++代码如下:
2
3
4
5
6
7
8
9
10
11
12class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
vector<int> dp(cost.size() + 1);
dp[0] = 0; // 默认第一步都是不花费体力的
dp[1] = 0;
for (int i = 2; i <= cost.size(); i++) {
dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
}
return dp[cost.size()];
}
};
- 时间复杂度:O(n)
- 空间复杂度:O(n)
还可以优化空间复杂度,因为
dp[i]就是由前两位推出来的,那么也不用dp数组了,C++代码如下:
2
3
4
5
6
7
8
9
10
11
12
13
14// 版本二
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
int dp0 = 0;
int dp1 = 0;
for (int i = 2; i <= cost.size(); i++) {
int dpi = min(dp1 + cost[i - 1], dp0 + cost[i - 2]);
dp0 = dp1; // 记录一下前两位
dp1 = dpi;
}
return dp1;
}
};
- 时间复杂度:O(n)
- 空间复杂度:O(1)
当然如果在面试中,能写出版本一就行,除非面试官额外要求 空间复杂度,那么再去思考版本二,因为版本二还是有点绕。版本一才是正常思路。
拓展
旧力扣描述,如果按照 第一步是花费的,最后一步不花费,那么代码是这么写的,提交也可以通过
2
3
4
5
6
7
8
9
10
11
12
13
14// 版本一
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
vector<int> dp(cost.size());
dp[0] = cost[0]; // 第一步有花费
dp[1] = cost[1];
for (int i = 2; i < cost.size(); i++) {
dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i];
}
// 注意最后一步可以理解为不用花费,所以取倒数第一步,第二步的最少值
return min(dp[cost.size() - 1], dp[cost.size() - 2]);
}
};当然如果对 动态规划 理解不够深入的话,拓展内容就别看了,容易越看越懵。
总结
大家可以发现这道题目相对于 昨天的动态规划:爬楼梯 (opens new window)又难了一点,但整体思路是一样的。
从动态规划:斐波那契数 (opens new window)到 动态规划:爬楼梯 (opens new window)再到今天这道题目,录友们感受到循序渐进的梯度了嘛。
每个系列开始的时候,都有录友和我反馈说题目太简单了,赶紧上难度,但也有录友和我说有点难了,快跟不上了。
其实我选的题目都是有目的性的,就算是简单题,也是为了练习方法论,然后难度都是梯度上来的,一环扣一环。
但我也可以随便选来一道难题讲呗,这其实是最省事的,不用管什么题目顺序,看心情找一道就讲。
难的是把题目按梯度排好,循序渐进,再按照统一方法论把这些都串起来,所以大家不要催我哈,按照我的节奏一步一步来就行了。
62.不同路径
题意描述:
[!WARNING]
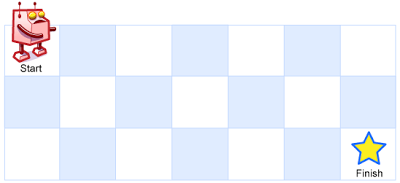
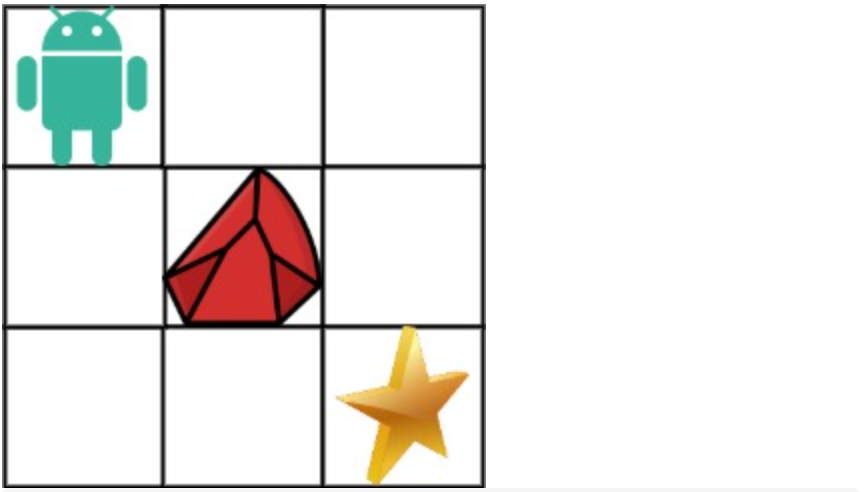
一个机器人位于一个
m x n网格的左上角 (起始点在下图中标记为 “Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
2输入:m = 3, n = 7
输出:28示例 2:
2
3
4
5
6
7输入:m = 3, n = 2
输出:3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下示例 3:
2输入:m = 7, n = 3
输出:28示例 4:
2输入:m = 3, n = 3
输出:6提示:
1 <= m, n <= 100- 题目数据保证答案小于等于(2 * 10^9^)
思路:
[!TIP]
深搜
这道题目,刚一看最直观的想法就是用图论里的深搜,来枚举出来有多少种路径。
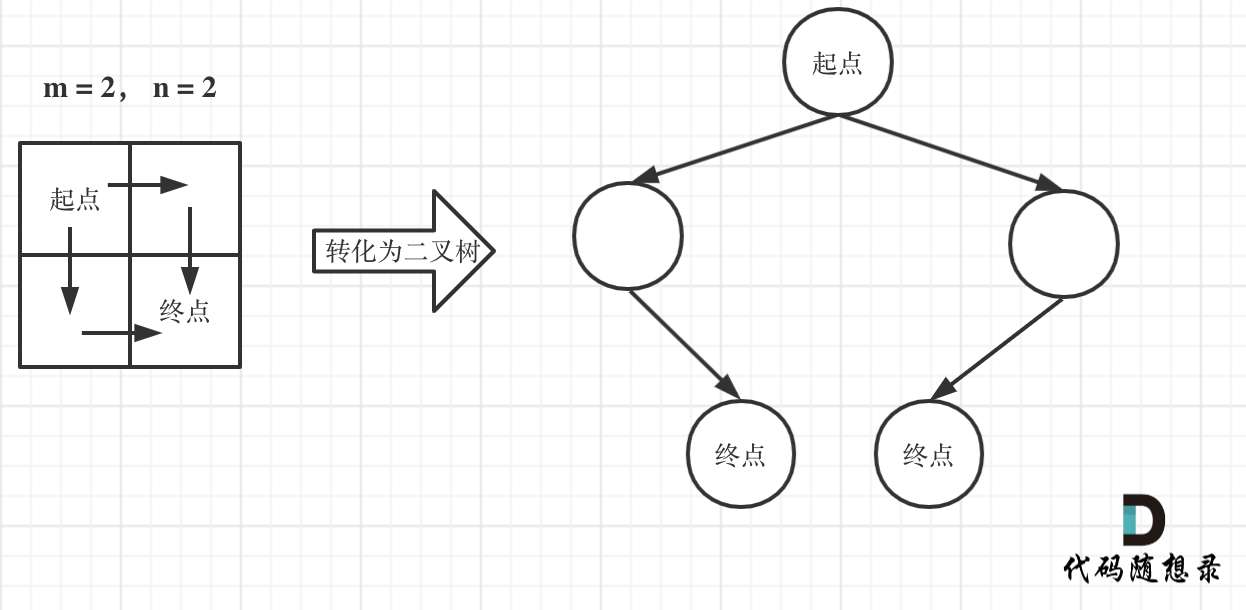
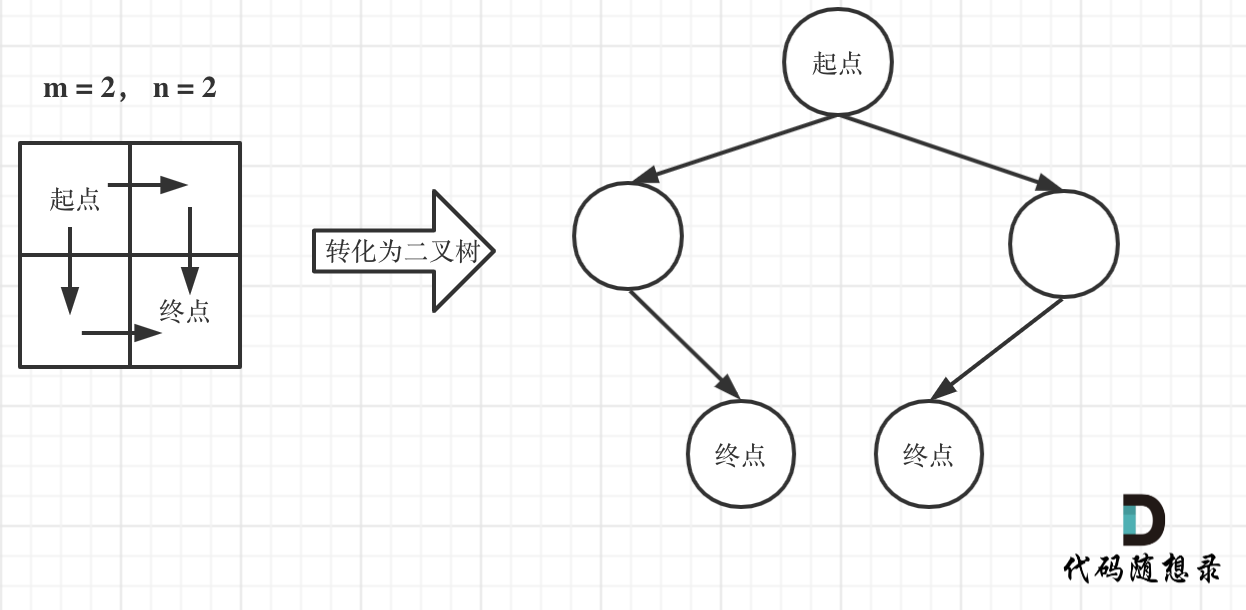
注意题目中说机器人每次只能向下或者向右移动一步,那么其实机器人走过的路径可以抽象为一棵二叉树,而叶子节点就是终点!
如图举例:
此时问题就可以转化为求二叉树叶子节点的个数,代码如下:
2
3
4
5
6
7
8
9
10
11
12class Solution {
private:
int dfs(int i, int j, int m, int n) {
if (i > m || j > n) return 0; // 越界了
if (i == m && j == n) return 1; // 找到一种方法,相当于找到了叶子节点
return dfs(i + 1, j, m, n) + dfs(i, j + 1, m, n);
}
public:
int uniquePaths(int m, int n) {
return dfs(1, 1, m, n);
}
};大家如果提交了代码就会发现超时了!
来分析一下时间复杂度,这个深搜的算法,其实就是要遍历整个二叉树。
这棵树的深度其实就是m+n-1(深度按从1开始计算)。
那二叉树的节点个数就是 2^(m + n - 1) - 1。可以理解深搜的算法就是遍历了整个满二叉树(其实没有遍历整个满二叉树,只是近似而已)
所以上面深搜代码的时间复杂度为O(2^(m + n - 1) - 1),可以看出,这是指数级别的时间复杂度,是非常大的。
)动态规划
机器人从(0 , 0) 位置出发,到(m - 1, n - 1)终点。
按照动规五部曲来分析:
- 确定dp数组(dp table)以及下标的含义
dp[i] [j] :表示从(0 ,0)出发,到(i, j) 有dp[i] [j]条不同的路径。
- 确定递推公式
想要求dp[i] [j],只能有两个方向来推导出来,即dp[i - 1] [j] 和 dp[i] [j - 1]。
此时在回顾一下 dp[i - 1] [j] 表示啥,是从(0, 0)的位置到(i - 1, j)有几条路径,dp[i] [j - 1]同理。
那么很自然,dp[i] [j] = dp[i - 1] [j] + dp[i] [j - 1],因为dp[i] [j]只有这两个方向过来。
- dp数组的初始化
如何初始化呢,首先dp[i] [0]一定都是1,因为从(0, 0)的位置到(i, 0)的路径只有一条,那么dp[0] [j]也同理。
所以初始化代码为:
2for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;
- 确定遍历顺序
这里要看一下递推公式dp[i] [j] = dp[i - 1] [j] + dp[i] [j - 1],dp[i] [j]都是从其上方和左方推导而来,那么从左到右一层一层遍历就可以了。
这样就可以保证推导dp[i] [j]的时候,dp[i - 1] [j] 和 dp[i] [j - 1]一定是有数值的。
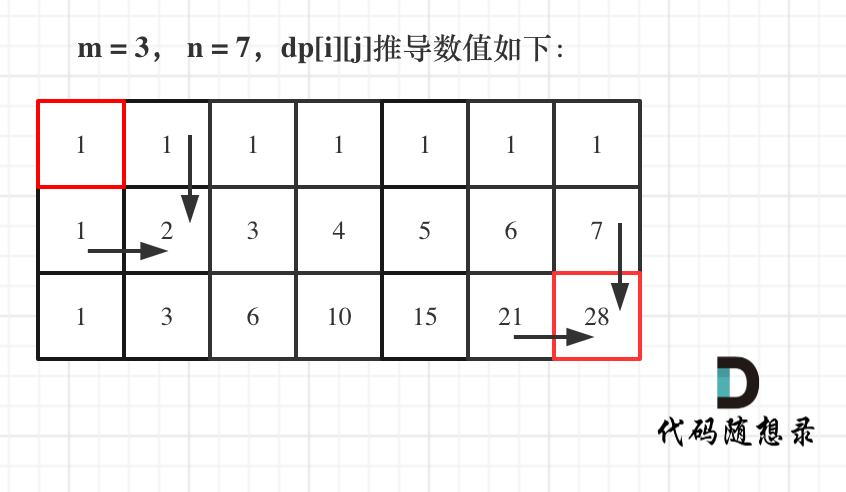
- 举例推导dp数组
如图所示:
以上动规五部曲分析完毕,C++代码如下:
2
3
4
5
6
7
8
9
10
11
12
13
14class Solution {
public:
int uniquePaths(int m, int n) {
vector<vector<int>> dp(m, vector<int>(n, 0));
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
};
- 时间复杂度:O(m × n)
- 空间复杂度:O(m × n)
其实用一个一维数组(也可以理解是滚动数组)就可以了,但是不利于理解,可以优化点空间,建议先理解了二维,在理解一维,C++代码如下:
2
3
4
5
6
7
8
9
10
11
12
13class Solution {
public:
int uniquePaths(int m, int n) {
vector<int> dp(n);
for (int i = 0; i < n; i++) dp[i] = 1;
for (int j = 1; j < m; j++) {
for (int i = 1; i < n; i++) {
dp[i] += dp[i - 1];
}
}
return dp[n - 1];
}
};
- 时间复杂度:O(m × n)
- 空间复杂度:O(n)
数论方法
在这个图中,可以看出一共m,n的话,无论怎么走,走到终点都需要 m + n - 2 步。
在这m + n - 2 步中,一定有 m - 1 步是要向下走的,不用管什么时候向下走。
那么有几种走法呢? 可以转化为,给你m + n - 2个不同的数,随便取m - 1个数,有几种取法。
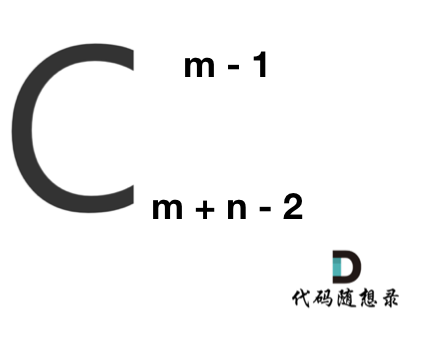
那么这就是一个组合问题了。
那么答案,如图所示:
求组合的时候,要防止两个int相乘溢出! 所以不能把算式的分子都算出来,分母都算出来再做除法。
例如如下代码是不行的。
2
3
4
5
6
7
8
9
10
11class Solution {
public:
int uniquePaths(int m, int n) {
int numerator = 1, denominator = 1;
int count = m - 1;
int t = m + n - 2;
while (count--) numerator *= (t--); // 计算分子,此时分子就会溢出
for (int i = 1; i <= m - 1; i++) denominator *= i; // 计算分母
return numerator / denominator;
}
};需要在计算分子的时候,不断除以分母,代码如下:
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
int uniquePaths(int m, int n) {
long long numerator = 1; // 分子
int denominator = m - 1; // 分母
int count = m - 1;
int t = m + n - 2;
while (count--) {
numerator *= (t--);
while (denominator != 0 && numerator % denominator == 0) {
numerator /= denominator;
denominator--;
}
}
return numerator;
}
};
- 时间复杂度:O(m)
- 空间复杂度:O(1)
计算组合问题的代码还是有难度的,特别是处理溢出的情况!
总结
本文分别给出了深搜,动规,数论三种方法。
深搜当然是超时了,顺便分析了一下使用深搜的时间复杂度,就可以看出为什么超时了。
然后在给出动规的方法,依然是使用动规五部曲,这次我们就要考虑如何正确的初始化了,初始化和遍历顺序其实也很重要!
63. 不同路径 II
题意描述:
[!WARNING]
一个机器人位于一个
m x n网格的左上角 (起始点在下图中标记为 “Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用
1和0来表示。示例 1:
2
3
4
5
6输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出:2
解释:3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右示例 2:
2输入:obstacleGrid = [[0,1],[0,0]]
输出:1提示:
m == obstacleGrid.lengthn == obstacleGrid[i].length1 <= m, n <= 100obstacleGrid[i][j]为0或1
思路:
[!TIP]
这道题相对于62.不同路径 (opens new window)就是有了障碍。
第一次接触这种题目的同学可能会有点懵,这有障碍了,应该怎么算呢?
62.不同路径 (opens new window)中我们已经详细分析了没有障碍的情况,有障碍的话,其实就是标记对应的dp table(dp数组)保持初始值(0)就可以了。
动规五部曲:
- 确定dp数组(dp table)以及下标的含义
dp[i] [j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
- 确定递推公式
递推公式和62.不同路径一样,
dp[i] [j] = dp[i - 1] [j] + dp[i] [j - 1]。但这里需要注意一点,因为有了障碍,(i, j)如果就是障碍的话应该就保持初始状态(初始状态为0)。
所以代码为:
2
3if (obstacleGrid[i][j] == 0) { // 当(i, j)没有障碍的时候,再推导dp[i][j]
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
- dp数组如何初始化
在62.不同路径 (opens new window)不同路径中我们给出如下的初始化:
2
3vector<vector<int>> dp(m, vector<int>(n, 0)); // 初始值为0
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;因为从(0, 0)的位置到(i, 0)的路径只有一条,所以dp[i] [0]一定为1,dp[0] [j]也同理。
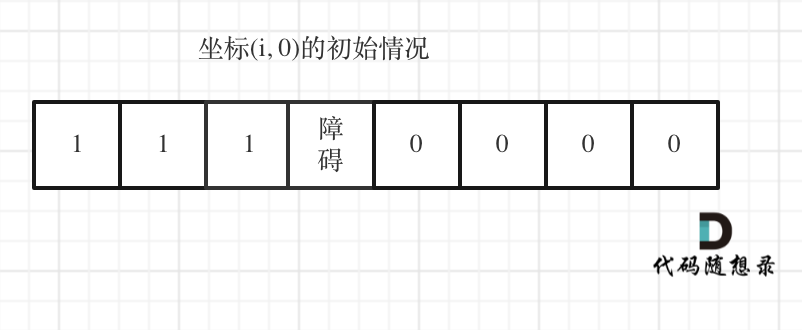
但如果(i, 0) 这条边有了障碍之后,障碍之后(包括障碍)都是走不到的位置了,所以障碍之后的dp[i] [0]应该还是初始值0。
如图:
下标(0, j)的初始化情况同理。
所以本题初始化代码为:
2
3vector<vector<int>> dp(m, vector<int>(n, 0));
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;注意代码里for循环的终止条件,一旦遇到
obstacleGrid[i] [0] == 1的情况就停止dp[i] [0]的赋值1的操作,dp[0] [j]同理
- 确定遍历顺序
从递归公式
dp[i] [j] = dp[i - 1] [j] + dp[i] [j - 1]中可以看出,一定是从左到右一层一层遍历,这样保证推导dp[i] [j]的时候,dp[i - 1] [j]和dp[i] [j - 1]一定是有数值。代码如下:
2
3
4
5
6for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (obstacleGrid[i][j] == 1) continue;
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
- 举例推导dp数组
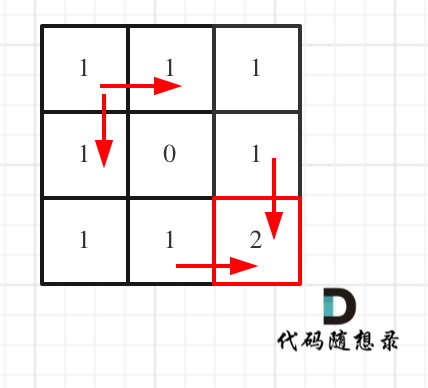
拿示例1来举例如题:
对应的dp table 如图:
如果这个图看不懂,建议再理解一下递归公式,然后照着文章中说的遍历顺序,自己推导一下!
动规五部分分析完毕,对应C++代码如下:
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
int m = obstacleGrid.size();
int n = obstacleGrid[0].size();
if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) //如果在起点或终点出现了障碍,直接返回0
return 0;
vector<vector<int>> dp(m, vector<int>(n, 0));
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (obstacleGrid[i][j] == 1) continue;
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
};
- 时间复杂度:O(n × m),n、m 分别为obstacleGrid 长度和宽度
- 空间复杂度:O(n × m)
同样我们给出空间优化版本:
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
if (obstacleGrid[0][0] == 1)
return 0;
vector<int> dp(obstacleGrid[0].size());
for (int j = 0; j < dp.size(); ++j)
if (obstacleGrid[0][j] == 1)
dp[j] = 0;
else if (j == 0)
dp[j] = 1;
else
dp[j] = dp[j-1];
for (int i = 1; i < obstacleGrid.size(); ++i)
for (int j = 0; j < dp.size(); ++j){
if (obstacleGrid[i][j] == 1)
dp[j] = 0;
else if (j != 0)
dp[j] = dp[j] + dp[j-1];
}
return dp.back();
}
};
- 时间复杂度:O(n × m),n、m 分别为
obstacleGrid长度和宽度- 空间复杂度:O(m)
总结
本题是62.不同路径 (opens new window)的障碍版,整体思路大体一致。
但就算是做过62.不同路径,在做本题也会有感觉遇到障碍无从下手。
其实只要考虑到,遇到障碍dp[i] [j]保持0就可以了。
也有一些小细节,例如:初始化的部分,很容易忽略了障碍之后应该都是0的情况。
343. 整数拆分
题意描述:
[!NOTE]
给定一个正整数
n,将其拆分为k个 正整数 的和(k >= 2),并使这些整数的乘积最大化。返回 你可以获得的最大乘积 。
示例 1:
2
3输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。示例 2:
2
3输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。提示:
2 <= n <= 58
思路:
[!TIP]
看到这道题目,都会想拆成两个呢,还是三个呢,还是四个….我们来看一下如何使用动规来解决。
动态规划
动规五部曲,分析如下:
- 确定dp数组(dp table)以及下标的含义
dp[i]:分拆数字i,可以得到的最大乘积为dp[i]。
dp[i]的定义将贯彻整个解题过程,下面哪一步想不懂了,就想想dp[i]究竟表示的是啥!
- 确定递推公式
可以想
dp[i]最大乘积是怎么得到的呢?其实可以从1遍历j,然后有两种渠道得到dp[i].一个是
j * (i - j)直接相乘。一个是
j * dp[i - j],相当于是拆分(i - j),对这个拆分不理解的话,可以回想dp数组的定义。那有同学问了,j怎么就不拆分呢?
j是从1开始遍历,拆分j的情况,在遍历j的过程中其实都计算过了。那么从1遍历j,比较
(i - j) * j和dp[i - j] * j取最大的。递推公式:dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));也可以这么理解,
j * (i - j)是单纯的把整数拆分为两个数相乘,而j * dp[i - j]是拆分成两个以及两个以上的个数相乘。如果定义
dp[i - j] * dp[j]也是默认将一个数强制拆成4份以及4份以上了。所以递推公式:
dp[i] = max({dp[i], (i - j) * j, dp[i - j] * j});那么在取最大值的时候,为什么还要比较dp[i]呢?因为在递推公式推导的过程中,每次计算dp[i],取最大的而已。
- dp的初始化
不少同学应该疑惑,
dp[0] dp[1]应该初始化多少呢?有的题解里会给出
dp[0] = 1,dp[1] = 1的初始化,但解释比较牵强,主要还是因为这么初始化可以把题目过了。严格从dp[i]的定义来说,dp[0] dp[1] 就不应该初始化,也就是没有意义的数值。
拆分0和拆分1的最大乘积是多少?
这是无解的。
这里我只初始化dp[2] = 1,从dp[i]的定义来说,拆分数字2,得到的最大乘积是1,这个没有任何异议!
- 确定遍历顺序
确定遍历顺序,先来看看递归公式:
dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
dp[i]是依靠dp[i - j]的状态,所以遍历i一定是从前向后遍历,先有dp[i - j]再有dp[i]。所以遍历顺序为:
2
3
4
5for (int i = 3; i <= n ; i++) {
for (int j = 1; j < i - 1; j++) {
dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
}
}注意 枚举j的时候,是从1开始的。从0开始的话,那么让拆分一个数拆个0,求最大乘积就没有意义了。
j的结束条件是
j < i - 1,其实j < i也是可以的,不过可以节省一步,例如让j = i - 1,的话,其实在 j = 1的时候,这一步就已经拆出来了,重复计算,所以j < i - 1至于 i是从3开始,这样
dp[i - j]就是dp[2]正好可以通过我们初始化的数值求出来。更优化一步,可以这样:
2
3
4
5for (int i = 3; i <= n ; i++) {
for (int j = 1; j <= i / 2; j++) {
dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
}
}因为拆分一个数n 使之乘积最大,那么一定是拆分成m个近似相同的子数相乘才是最大的。
例如 6 拆成 3 3, 10 拆成 3 3 * 4。 100的话 也是拆成m个近似数组的子数 相乘才是最大的。
只不过我们不知道m究竟是多少而已,但可以明确的是m一定大于等于2,既然m大于等于2,也就是 最差也应该是拆成两个相同的 可能是最大值。那么 j 遍历,只需要遍历到 n/2 就可以,后面就没有必要遍历了,一定不是最大值。
至于 “拆分一个数n 使之乘积最大,那么一定是拆分成m个近似相同的子数相乘才是最大的” 这个我就不去做数学证明了,感兴趣的同学,可以自己证明。
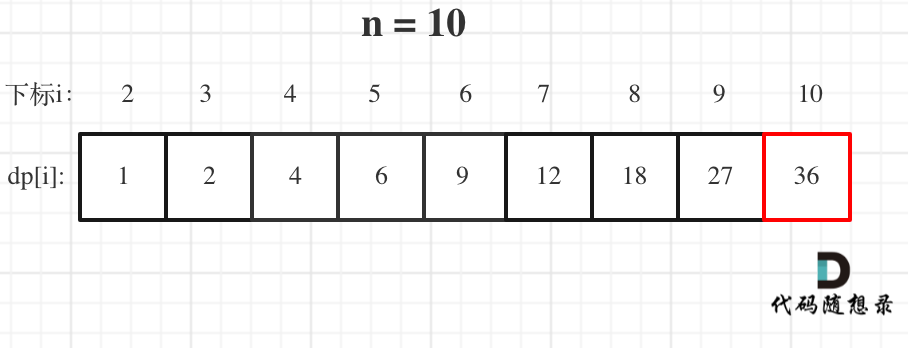
- 举例推导dp数组
举例当n为10 的时候,dp数组里的数值,如下:
以上动规五部曲分析完毕,C++代码如下:
2
3
4
5
6
7
8
9
10
11
12
13class Solution {
public:
int integerBreak(int n) {
vector<int> dp(n + 1);
dp[2] = 1;
for (int i = 3; i <= n ; i++) {
for (int j = 1; j <= i / 2; j++) {
dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
}
}
return dp[n];
}
};
- 时间复杂度:O(n^2)
- 空间复杂度:O(n)
贪心
本题也可以用贪心,每次拆成n个3,如果剩下是4,则保留4,然后相乘,但是这个结论需要数学证明其合理性!
我没有证明,而是直接用了结论。感兴趣的同学可以自己再去研究研究数学证明哈。
给出我的C++代码如下:
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
int integerBreak(int n) {
if (n == 2) return 1;
if (n == 3) return 2;
if (n == 4) return 4;
int result = 1;
while (n > 4) {
result *= 3;
n -= 3;
}
result *= n;
return result;
}
};
- 时间复杂度:O(n)
- 空间复杂度:O(1)
总结
本题掌握其动规的方法,就可以了,贪心的解法确实简单,但需要有数学证明,如果能自圆其说也是可以的。
其实这道题目的递推公式并不好想,而且初始化的地方也很有讲究,我在写本题的时候一开始写的代码是这样的:
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
public:
int integerBreak(int n) {
if (n <= 3) return 1 * (n - 1);
vector<int> dp(n + 1, 0);
dp[1] = 1;
dp[2] = 2;
dp[3] = 3;
for (int i = 4; i <= n ; i++) {
for (int j = 1; j <= i / 2; j++) {
dp[i] = max(dp[i], dp[i - j] * dp[j]);
}
}
return dp[n];
}
};这个代码也是可以过的!
在解释递推公式的时候,也可以解释通,dp[i] 就等于 拆解i - j的最大乘积 * 拆解j的最大乘积。 看起来没毛病!
但是在解释初始化的时候,就发现自相矛盾了,dp[1]为什么一定是1呢?根据dp[i]的定义,dp[2]也不应该是2啊。
但如果递归公式是 dp[i] = max(dp[i], dp[i - j] * dp[j]);,就一定要这么初始化。递推公式没毛病,但初始化解释不通!
虽然代码在初始位置有一个判断if (n <= 3) return 1 (n - 1);,保证n<=3 结果是正确的,但代码后面又要给dp[1]赋值1 和 dp[2] 赋值 2,*这其实就是自相矛盾的代码,违背了dp[i]的定义!
我举这个例子,其实就说做题的严谨性,上面这个代码也可以AC,大体上一看好像也没有毛病,递推公式也说得过去,但是仅仅是恰巧过了而已。
96.不同的二叉搜索树
题意描述:
[!WARNING]
给你一个整数
n,求恰由n个节点组成且节点值从1到n互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。示例 1:
2输入:n = 3
输出:5示例 2:
2输入:n = 1
输出:1提示:
1 <= n <= 19
思路:
[!TIP]
这道题目描述很简短,但估计大部分同学看完都是懵懵的状态,这得怎么统计呢?
关于什么是二叉搜索树,我们之前在讲解二叉树专题的时候已经详细讲解过了,也可以看看这篇二叉树:二叉搜索树登场! (opens new window)再回顾一波。
了解了二叉搜索树之后,我们应该先举几个例子,画画图,看看有没有什么规律,如图:
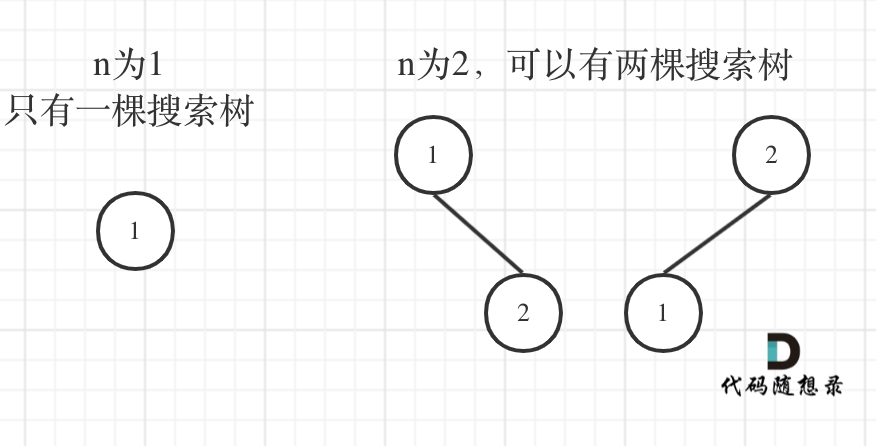
n为1的时候有一棵树,n为2有两棵树,这个是很直观的。
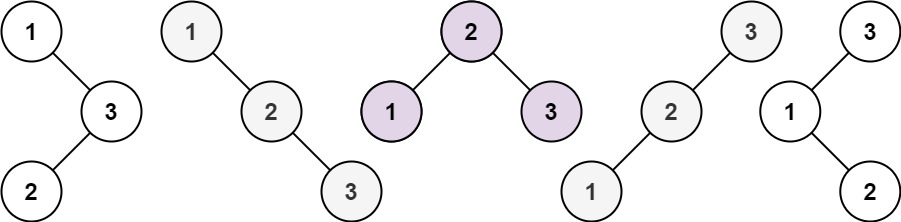
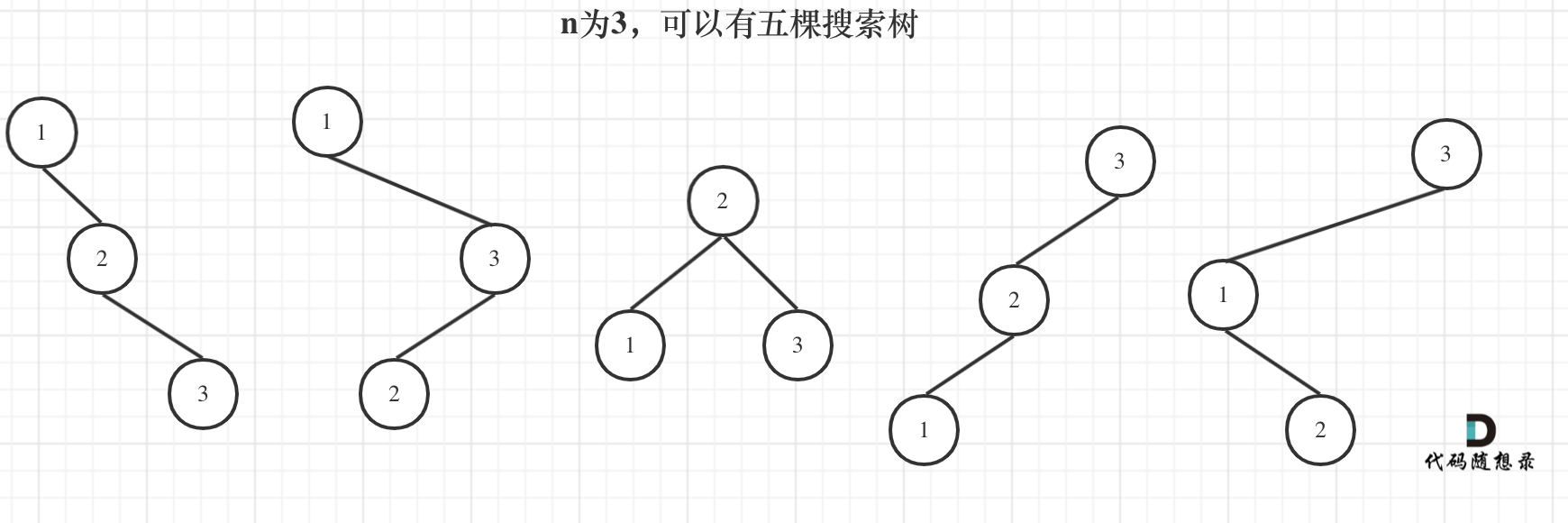
来看看n为3的时候,有哪几种情况。
当1为头结点的时候,其右子树有两个节点,看这两个节点的布局,是不是和 n 为2的时候两棵树的布局是一样的啊!
(可能有同学问了,这布局不一样啊,节点数值都不一样。别忘了我们就是求不同树的数量,并不用把搜索树都列出来,所以不用关心其具体数值的差异)
当3为头结点的时候,其左子树有两个节点,看这两个节点的布局,是不是和n为2的时候两棵树的布局也是一样的啊!
当2为头结点的时候,其左右子树都只有一个节点,布局是不是和n为1的时候只有一棵树的布局也是一样的啊!
发现到这里,其实我们就找到了重叠子问题了,其实也就是发现可以通过dp[1] 和 dp[2] 来推导出来dp[3]的某种方式。
思考到这里,这道题目就有眉目了。
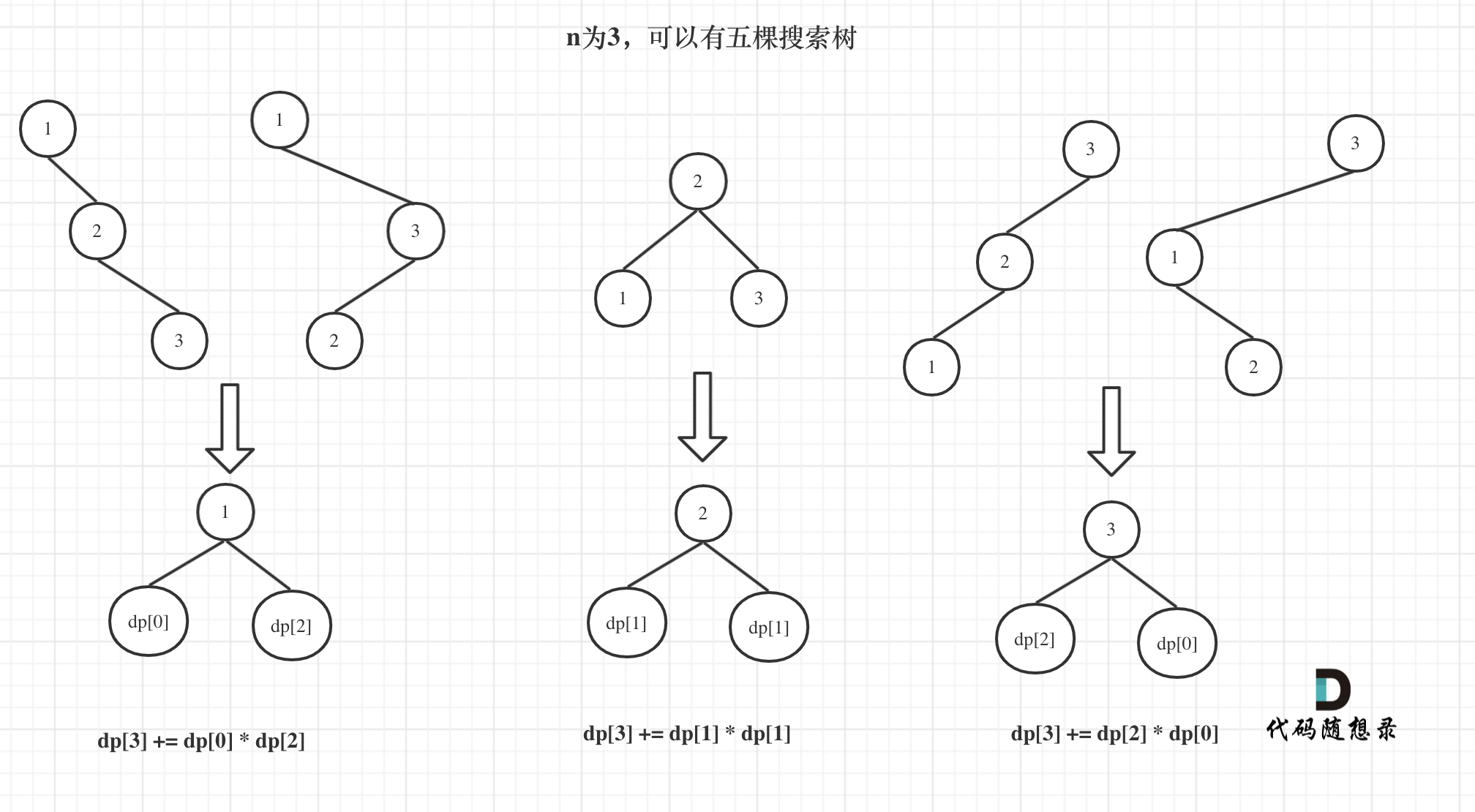
dp[3] = 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量
元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量
元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量
元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量
有2个元素的搜索树数量就是dp[2]。
有1个元素的搜索树数量就是dp[1]。
有0个元素的搜索树数量就是dp[0]。
所以dp[3] = dp[2] dp[0] + dp[1] dp[1] + dp[0] * dp[2]
如图所示:
此时我们已经找到递推关系了,那么可以用动规五部曲再系统分析一遍。
- 确定dp数组(dp table)以及下标的含义
dp[i] : 1到i为节点组成的二叉搜索树的个数为dp[i]。
也可以理解是i个不同元素节点组成的二叉搜索树的个数为dp[i] ,都是一样的。
以下分析如果想不清楚,就来回想一下dp[i]的定义
- 确定递推公式
在上面的分析中,其实已经看出其递推关系,
dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]j相当于是头结点的元素,从1遍历到i为止。
所以递推公式:
dp[i] += dp[j - 1] * dp[i - j]; ,j-1 为j为头结点左子树节点数量,i-j 为以j为头结点右子树节点数量
- dp数组如何初始化
初始化,只需要初始化dp[0]就可以了,推导的基础,都是dp[0]。
那么dp[0]应该是多少呢?
从定义上来讲,空节点也是一棵二叉树,也是一棵二叉搜索树,这是可以说得通的。
从递归公式上来讲,dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量] 中以j为头结点左子树节点数量为0,也需要dp[以j为头结点左子树节点数量] = 1, 否则乘法的结果就都变成0了。所以初始化dp[0] = 1
- 确定遍历顺序
首先一定是遍历节点数,从递归公式:
dp[i] += dp[j - 1] * dp[i - j]可以看出,节点数为i的状态是依靠 i之前节点数的状态。那么遍历i里面每一个数作为头结点的状态,用j来遍历。
代码如下:
2
3
4
5for (int i = 1; i <= n; i++) {
for (int j = 1; j <= i; j++) {
dp[i] += dp[j - 1] * dp[i - j];
}
}
- 举例推导dp数组
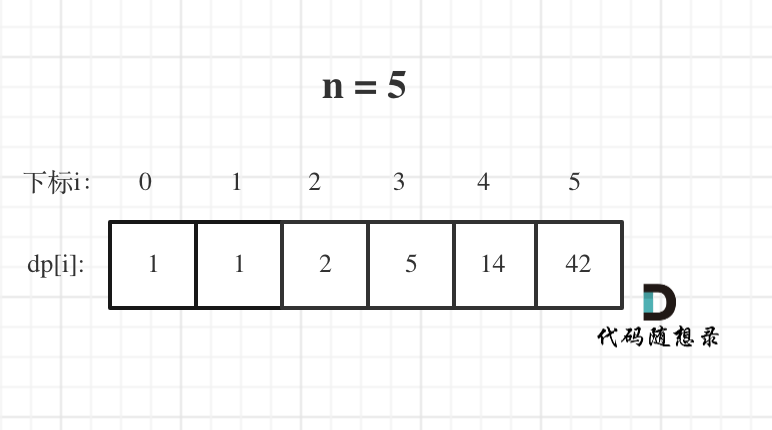
n为5时候的dp数组状态如图:
当然如果自己画图举例的话,基本举例到n为3就可以了,n为4的时候,画图已经比较麻烦了。
我这里列到了n为5的情况,是为了方便大家 debug代码的时候,把dp数组打出来,看看哪里有问题。
综上分析完毕,C++代码如下:
2
3
4
5
6
7
8
9
10
11
12
13class Solution {
public:
int numTrees(int n) {
vector<int> dp(n + 1);
dp[0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= i; j++) {
dp[i] += dp[j - 1] * dp[i - j];
}
}
return dp[n];
}
};
- 时间复杂度:$O(n^2)$
- 空间复杂度:$O(n)$
大家应该发现了,我们分析了这么多,最后代码却如此简单!
总结
这道题目虽然在力扣上标记是中等难度,但可以算是困难了!
首先这道题想到用动规的方法来解决,就不太好想,需要举例,画图,分析,才能找到递推的关系。
然后难点就是确定递推公式了,如果把递推公式想清楚了,遍历顺序和初始化,就是自然而然的事情了。
可以看出我依然还是用动规五部曲来进行分析,会把题目的方方面面都覆盖到!
而且具体这五部分析是我自己平时总结的经验,找不出来第二个的,可能过一阵子 其他题解也会有动规五部曲了。
当时我在用动规五部曲讲解斐波那契的时候,一些录友和我反应,感觉讲复杂了。
其实当时我一直强调简单题是用来练习方法论的,并不能因为简单我就代码一甩,简单解释一下就完事了。
可能当时一些同学不理解,现在大家应该感受方法论的重要性了,加油💪
[动态规划:01背包理论基础]
题意描述:
[!NOTE]
有 𝑁 件物品和一个容量是 𝑉 的背包。每件物品只能使用一次。
第 𝑖 件物品的体积是 𝑣𝑖,价值是 𝑤𝑖。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。输入格式
第一行两个整数,𝑁,𝑉,用空格隔开,分别表示物品数量和背包容积。
接下来有 𝑁 行,每行两个整数𝑣𝑖,𝑤𝑖,用空格隔开,分别表示第 𝑖 件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<𝑁,𝑉≤1000
0<𝑣𝑖,𝑤𝑖≤1000输入样例
2
3
4
54 5
1 2
2 4
3 4
4 5输出样例:
8
思路:
[!TIP]